十一刚刚玩完心还是飞的,写了几场比赛,感觉状态不是很好,把遇到的比较好问题写在这里。(不知道为啥最近遇到的大多都是计数问题)
之前一直在忙找工作,还算运气好投了4个,收了3个。以后应该就在上海了。
也不知道以后工作了还有没有时间打比赛。
数学考试
题目要求我们计数:一个n个数的排列,现在有m个restriction \(p_i\),每个restriction要求前\(p_i\)个数不能是\(p_i\)的排列,求总方案数(对mod取模)。
典型的dp计数问题,想到了状态但是没有理清转移方程。
首先我们把\(p_i\)按照从小到大排序。
计\(dp[i]\)为当前有\(p_i\)个元素时,前i-1个条件\(p_k, k \ from\ 1 \ to \ i-1\)全部满足的方案数。发现我们只要在p数组的最后一个位置填上n,这样\(dp[m+1]\)即为我们的答案。
当我们计算\(dp[i]\)时,需要从\(p_i!\)中减去之前重复的部分,我们可以把所有排列分成若干个部分,每次减去:是\(p_j\)的排列但不是\(p_{1~j-1}\)的排列,这样就有 \[ dp[i]=p[i]! - \sum_{j=1}^{i-1} (p[i]-p[j])! * p[i] \] 最终可得答案。
Fair Elevator
总共有2n层楼,每层都只有一个人上或者下,现在给你n个人的记录A,B:A代表在A层上电梯,B代表在B层下电梯。
他们上下电梯时遵循一种奇怪的原则:同时在电梯里面的人,所乘坐的层数是相同的(若i,j在电梯中相遇,则有\(B_i-A_i==B_j-A_j\))
目前由于少了一些记录(用-1)代替,问这个记录是否合法?(或者说是否存在一种可能,替换所有-1为任意数字,使得记录满足上面的条件)
首先我们可以发现,根据题目条件,每一层楼必有一人上或者下。
我们用\(x,x+k\)来表示在x层上,在x+k层下,此时根据题目条件,可以发现必有\((x+1,x+k+1),(x+2,x+k+2),…(x+k-1,x+2k-1)\)。
也就是说如果\((x,x+k)\)如果是第一个上电梯的人,我们可以像数学归纳法一样得知后面k-1个人的上下情况。
接下来我们可以用dp来求解这个问题:用\(bool\ dp[i]\)来表示1到第i个位置是否存在一种合法的解决方案,0表示不合法,1表示合法。
\(dp[i]=dp[j]\ \& \ f[j,i]\ (j < i)\)其中\(f[j,i]\)表示j到i是否有一种方案能够合法。
说实话方程很朴素,但是实现很抽象。实现可以参考标程中的实现
方案是记录每个位置的属性,比如是否是左端点,右端点,是否有对应点,方便我们讨论\(f[j,i]\)的值。
Squares
仍是一个计数问题,问在一个边长为n的正方形网格图内填充两个小正方形,边长分别为a和b,小正方形的顶点必须在格点上。n,a,b都是正整数,问有多少种方案数满足两个小正方形不重叠。
首先,当一个边长为a的正方形放在一个边长为n的正方形内时,总方案数为\((n-a+1)^2\),而且当n<a+b的时候一定无解。
那么我们不计算重叠时,总方案数为\(total=(n-a+1)^2*(n-b+1)^2\)
我们分情况讨论,正方形有四条边,重叠可能在边上可能在角上
在边上的时候:
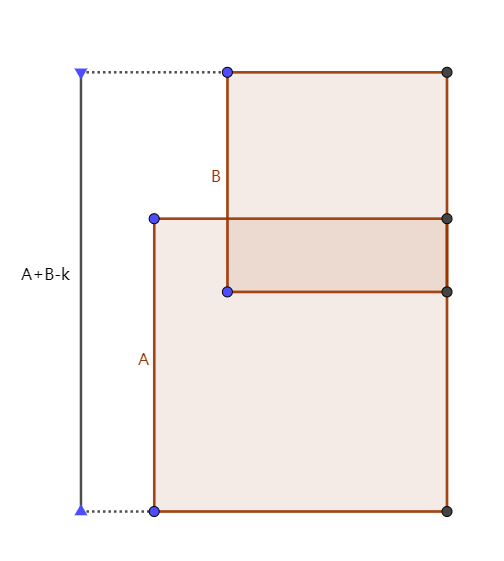
此种情况我们可以计算出在一边上的时候,重叠的总数为 \[ p1=(a-b+1)(n-a+1)*[(n+1)(b-1)-\frac{2a+b}{2}(b-1)] \]
在角上的时候:
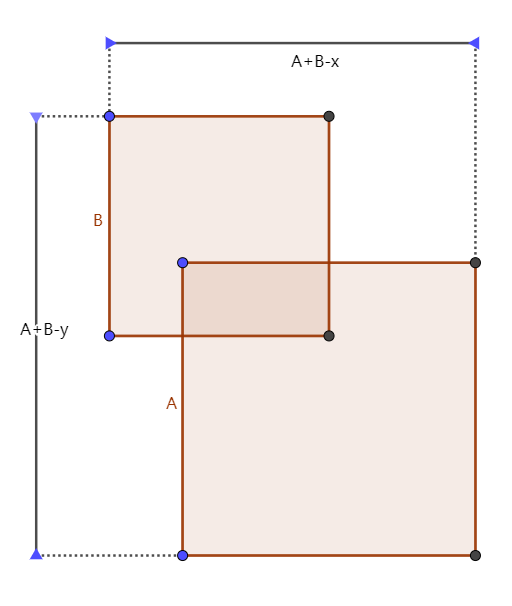
此种情况重叠的总数为 \[ p2=[(n+1)(b-1)-\frac{2a+b}{2}(b-1)]^2 \]
所以总数即为\(ans=total-4p1-4p2\)
Lamps
给你一个n*m的点阵,每个点阵为0或者是1,我们可以在为0的点上放台灯,这个台灯能点亮一些为0的区域:向上下左右四个方向延申,当遇到一个为1的点时停止。
现在给你这个点阵的状态,点阵中有k个为0的点,所以我们有\(2^k\)种放置的方式。求所有放置方案点亮区域的总和。
首先我们可以\(O(nm)\)预处理出一个点\((i,j)\)能够点亮的区域数,记为\(f_{ij}\)
发现正向计算非常不好算,我们反过来讨论每个点对答案的贡献。
一个点只会被同行同列能覆盖的点覆盖到,所以点\((i,j)\)对答案的贡献就是\( 2^{f_{i,j}-1}*2^{k-f_{ij}} \)
所以答案就是累加所有为0的点的贡献 \[ ans=\sum_{i,j \ map[i,j]=0} 2^{f_{ij}-1}*2^{k-f_{ij}} \]
Camels and Bridge
这个题给我感觉是最难的。
n个骆驼过桥,他们必须排成一列依次过桥,每个骆驼有个重量\(w_i\),桥也分成了m段,每个段有个最大承重,当桥上的骆驼总重量大于这个值的时候,这一段就会塌。
你现在可以任意指定骆驼的顺序,以及每两个骆驼之间的距离,需要找出这个骆驼队列的最小长度。
看到数据量的时候第一反应是枚举加二分,但是算了下时间不够。后面也没有想到好的做法。
以下是题解的做法:
当最重的骆驼无法通过承重最小的桥时,无解。
对于一个骆驼排列,算出\(x_{ij}\),表示在当前排列下,骆驼i,j之间的最小距离。这个可以在\(O(log^m)\)时间内解决
会发现这是一个有\(\frac{n(n-1)}{2}\)条边的DAG图,我们求出这个DAG的最长路即是该次排列下的答案。
这里的最长路很难理解:为什么不是最短路呢?
因为取最短路的话桥会塌掉嘛。最简单的,考虑下面这张图:
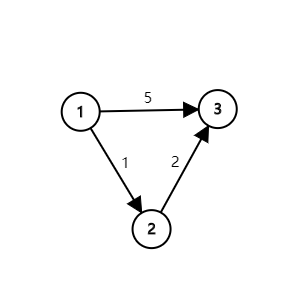
显而易见。